素数パズルで楽しく計算して数の感覚を身に付ける(３～５年生向け)

数の感覚を最も簡単に身につけられるパズル『素数パズル』を作成しました

数の感覚を身に付けるために最も効果があるのは『素因数分解』『最大公約数』です。

この二つが得意になると、数の問題はもちろん単純な計算が大きく改善するので算数全体の成績を底上げすることにつながります。

しかし問題はただ素因数分解や最大公約数を出させられ続けるのは子供にとっては退屈だということです。

もしこの単純な反復練習に楽しめるパズル要素があれば取り組む子も多くなるのではないか。

そう思って授業で取り入れたところ大成功、多くの子が積極的に取り組み算数が得意な子がたくさん現れました。

そんな素数パズルを公開します。

素数パズル紹介と解説

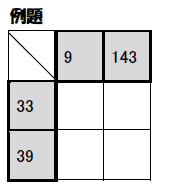
これはルールを理解するための例題です。

四角に入れたかずを縦にかけ算すると一番上の色がついた数、横にかけ算すると一番左の数になります。

同じ数は何回使ってもいいですが１は使えません。

どこからでも埋められるのですが、９＝３×３であることから９の下のマスが両方共３だとわかるとすぐに決まります。

白い四角には素数が入るのですが素数という言葉を未習の低学年であればあえておしえずそのまま解かせてもOKです。

６とかいれるとパズルが完成しないようにできているので問題ありません。素数を覚えるきっかけにもなります。

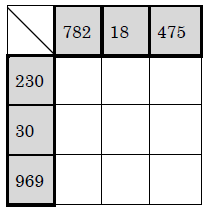
この問題が中難度です。

３つ登場すると一つの数だけみてもマスが埋まらないことが多いです。

今回だと横の数230と30が５で割れるのに対して、上の数は475しか５で割れません。

そのため230と475が交わるマスと230と30が交わるマスは５になります。

すると475÷５÷５で475の列の最後１マスも求められます。

わかったことを利用すると次にわかるマスが増えてきます。

順番に埋めていく中で自然にかけ算わり算を繰り返すことになります。

裏技としては先にすべての数を素因数分解してしまうと簡単に埋められるのですが、難易度が上がるとその素因数分解が容易ではなくなります。

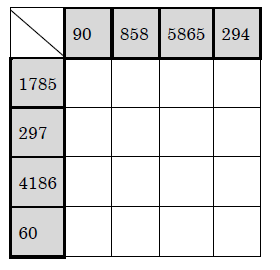
最高難度はこんな感じです。

解答の例としては

297＝3×3×3×11なので11の倍数が他に見つかれば一気に一行決まります。

11の倍数を探すと858なのでそこは11、それ以外は3

マスの数が３列になったところから解きやすいものを埋めていけば求めることができます。

このパズルを楽しんでいるうちに確実に数の感覚が鋭くなっていきます。

最初は中難度(２)のものだけ取り組むでも構いません。

ぜひ使ってみてください。

素数パズルはこちら

無料アプリnoteで作成しています。ぜひご覧下さい。

https://note.com/juken3su/n/n1b6f47ec8eb2

下はサンプルデータです。